Hier werden unveränderliche Sammlungen in einer Beispielrechnung veränderlichen Sammlungen gegenübergestellt.

Unveränderliche Sammlungen sind nützlich zum Schreiben purer Funktionen. Pure Funktionen sind threadsicher und oft einfach zu testen. Eine Eigenschaft purer Funktionen ist, dass sie ihre Eingabeargumente nicht verändern. Diese Eigenschaft kann man in der Signatur hervorheben durch die Nutzung unveränderlicher Typen.

Zum Beispiel hebt 

using System;
using System.Collections.Immutable;
...
public static ImmutableList<double> CalculateSomething(ImmutableList<double> input, int windowSize)
...

hervor, dass die Eingabesammlung durch die Rechnung nicht verändert wird.

Das Hinzufügen zu einer unveränderlichen Liste geht über die Add-Methode. Diese baut eine neue Liste mit dem hinzugefügten Wert und läßt die Ausgangsliste unverändert. Die gleiche Vorgehensweise gilt bei anderen unveränderlichen Sammlungen. Falls danach keine Referenzen zur Ausgangsliste zeigen, ist sie ein Fall für die nächste Müllabfuhr (GC, garbage collection). Kommt das öfters vor, durch häufiges Ändern, führt das zu einem Mehraufwand für die GC. Spürbare Leistungseinbußen können die Folge sein, wie Hadi Brais im MSDN-Magazin zeigte.

Spürbare Leistungseinbußen passieren zum Beispiel beim Berechnen des einfachen gleitenden Mittelwerts über 10⁷ Gleitzommazahlen mit einer Fensterbreite von 1500. Die Mittelwerte zu berechnen erfordert das Halten eines Fensters. Dazu eignet sich eine Warteschlange. Listen und Stapel eignen sich zum Aufsammeln der Mittelwerte. Der folgende Quelltext hat einige öffentliche Funktionen, die diese Rechnung durchführen können, jeweils mit verschiedenen Sammlungstypen. 

using System;
using System.Linq;
using System.Collections.Generic;
using System.Collections.Immutable;

namespace MovingAverage
{
    public static class Calculator
    {
        public static ImmutableList<double> CalculateWithImmutableQueueList(int windowSize, ImmutableList<double> input)
        => CalculateWithImmutableQueue(
            ImmutableList.Create<double>(),
            (list, next) => list.Add(next),
            windowSize,
            input).ToImmutableList();

        public static ImmutableList<double> CalculateWithImmutableQueueStack(int windowSize, ImmutableList<double> input)
        => CalculateWithImmutableQueue(
            ImmutableStack.Create<double>(),
            (stack, next) => stack.Push(next),
            windowSize,
            input).Reverse().ToImmutableList();

        public static ImmutableList<double> CalculateWithImmutableQueueAndMutableStack(int windowSize, ImmutableList<double> input)
        => CalculateWithImmutableQueue(
            new Stack<double>(),
            (stack, next) => { stack.Push(next); return stack; },
            windowSize,
            input).Reverse().ToImmutableList();

        public static ImmutableList<double> CalculateWithImmutableQueueAndMutableList(int windowSize, ImmutableList<double> input)
        => CalculateWithImmutableQueue(
            new List<double>(),
            (list, next) => { list.Add(next); return list; },
            windowSize,
            input).ToImmutableList();

        public static ImmutableList<double> CalculateWithQueueStack(int windowSize, ImmutableList<double> input)
        => CalculateWithMutableQueue(
            new Stack<double>(),
            (stack, next) => { stack.Push(next); return stack; },
            windowSize,
            input).Reverse().ToImmutableList();

        public static ImmutableList<double> CalculateWithQueueList(int windowSize, ImmutableList<double> input)
        => CalculateWithMutableQueue(
            new List<double>(),
            (list, next) => { list.Add(next); return list; },
            windowSize,
            input).ToImmutableList();

        static S CalculateWithImmutableQueue<S>(S emptyStack, Push<S> push, int windowSize, ImmutableList<double> input)
        => Calculate(
            ImmutableQueue<double>.Empty,
            (queue) => queue.Peek(),
            (queue, next) => queue.Enqueue(next),
            (queue) => queue.Dequeue(),
            emptyStack,
            push,
            windowSize,
            input);

        static S CalculateWithMutableQueue<S>(S emptyStack, Push<S> push, int windowSize, ImmutableList<double> input)
        => Calculate(
            new Queue<double>(),
            (queue) => queue.Peek(),
            (queue, next) => { queue.Enqueue(next); return queue; },
            (queue) => { _ = queue.Dequeue(); return queue; },
            emptyStack,
            push,
            windowSize,
            input);

        static S Calculate<Q, S>(
            Q emptyQueue,
            Peek<Q> peek,
            Enqueue<Q> enqueue,
            Dequeue<Q> dequeue,
            S emptyStack,
            Push<S> push,
            int windowSize,
            ImmutableList<double> input)
        {
            IEnumerable<double> head = input.Take(windowSize - 1);
            ImmutableList<double> tail = input.TakeLast(input.Count - (windowSize - 1)).ToImmutableList();

            Q headQueue = head.Aggregate(emptyQueue, (q, next) => enqueue(q, next));

            return tail.Aggregate((head.Sum(), headQueue, emptyStack), (state, next) =>
            {
                double sum = state.Item1 + next;
                Q queue = state.Item2;
                S stack = state.Item3;

                stack = push(stack, sum / windowSize);

                sum -= peek(queue); 
                queue = dequeue(queue);
                queue = enqueue(queue, next);

                return (sum, queue, stack);
            }).Item3;
        }

        delegate S Push<S>(S stack, double next);

        delegate Q Enqueue<Q>(Q queue, double next);

        delegate Q Dequeue<Q>(Q queue);

        delegate double Peek<Q>(Q queue);
    }
}

Die wesentlichen Schritte werden durch die private Calculate-Funktion ausgeführt Diese bekommt mehrere Delegaten um

Beim Schieben in einen Stack liegen die Mittelwerte am Ende in umgekehrter Reihenfolge vor. Das erfordert ein nachträgliches Umdrehen.

Der folgende Quelltext enthält einen Test zum Prüfen der Ergebnisse. Darüber hinaus enthält er einen weiteren Test zum Schätzen der Rechendauer. 

using System;
using System.Collections.Generic;
using System.Collections.Immutable;
using System.Linq;
using Xunit;
using static Xunit.Assert;
using static MovingAverage.Calculator;
using System.Diagnostics;
using static System.Diagnostics.Stopwatch;
using Xunit.Abstractions;
using System.Collections;

namespace MovingAverage.Test
{
    public class CalculatorTest
    {
        readonly ITestOutputHelper output;
        public CalculatorTest(ITestOutputHelper output)
        {
            this.output = output;
        }

        [Theory]
        [ClassData(typeof(TestArguments))]
        public void CheckMath(SmaCalculator smaCalculator, int windowSize)
        {
            const int n = 10_000;

            ImmutableList<double> input = GetRandomNumbers(n, -1, 1).ToImmutableList();
            ImmutableList<double> result = smaCalculator(windowSize, input);

            Equal(input.Count() - windowSize + 1, result.Count());
            Equal(input.Take(windowSize).Sum() / (double)windowSize, result.First(), 6);
            Equal(input.TakeLast(windowSize).Average(), result.Last(), 6);
        }

        [Theory]
        [ClassData(typeof(TestArguments))]
        public void MeasureDuration(SmaCalculator smaCalculator, int windowSize)
        {
            const int n = 10_000_000;

            ImmutableList<double> input = GetRandomNumbers(n, -1, 1).ToImmutableList();
            Measure(n, windowSize, () => _ = smaCalculator(windowSize, input));

            void Measure(int n, int k, Action calc)
            {
                Stopwatch sw = StartNew();
                calc();
                sw.Stop();
                double elapsedSeconds = sw.ElapsedMilliseconds / 1000.0;
                output.WriteLine("Calculating the moving averages with "
                    + $"{smaCalculator.Method.Name}, n = {n.ToString("e0")}, k = {k} took {elapsedSeconds.ToString("N3")}s.");
            }
        }

        public class TestArguments : IEnumerable<object[]>
        {
            public IEnumerator<object[]> GetEnumerator()
            {
                foreach (var p in GetParametersWithWindowSize(15)) yield return p;
                foreach (var p in GetParametersWithWindowSize(150)) yield return p;
                foreach (var p in GetParametersWithWindowSize(1500)) yield return p;
            }

            IEnumerable<object[]> GetParametersWithWindowSize(int windowSize)
            => ImmutableList.Create<object[]>
            (
                new object[] { (SmaCalculator)CalculateWithImmutableQueueList, windowSize },
                new object[] { (SmaCalculator)CalculateWithImmutableQueueStack, windowSize },
                new object[] { (SmaCalculator)CalculateWithImmutableQueueAndMutableStack, windowSize },
                new object[] { (SmaCalculator)CalculateWithImmutableQueueAndMutableList, windowSize },
                new object[] { (SmaCalculator)CalculateWithQueueStack, windowSize },
                new object[] { (SmaCalculator)CalculateWithQueueList, windowSize }
            );

            IEnumerator IEnumerable.GetEnumerator() => GetEnumerator();
        }

        static IEnumerable<double> GetRandomNumbers(int count, double from, double to)
        {
            Random r = new Random(0);
            return Enumerable.Range(0, count).Select(_ => from + (to - from) * r.NextDouble());
        }

        public delegate ImmutableList<double> SmaCalculator(int windowSize, ImmutableList<double> input);
    }
}

Ein Testlauf druckte folgende Werte zur Rechendauer

CalculateWith Fensterbreite 15 Fensterbreite 150 Fensterbreite 1500
ImmutableQueueList 11,4s 13,1s 11,6s
ImmutableQueueStack 5,4s 5,6s 5,4s
ImmutableQueueAndMutableStack 4,2s 3,8s 3,7s
ImmutableQueueAndMutableList 3,7s 3,8s 3,6s
QueueList 3,2s 3,4s 3,3s
QueueStack 3,2s 3,6s 3,3s

Aufsammeln mit einer unveränderlichen Liste dauert länger als mit einem Stabel. Eine Erklärung dafür liefert Hadi Brais im oben erwähnten Artikel: Der unveränderliche Stapel ist als verknüpfte-Liste implementiert und deren Push-Medthode ist aufwandsärmer als die Add methode der unveränderlichen Liste. Letztere ist als Binärbaum implementiert. Hinzufügen von Knoten

Um den GC-Mehraufwand zu sehen, habe ich drei der obigen Rechnungen mit PerfView laufen lassen.

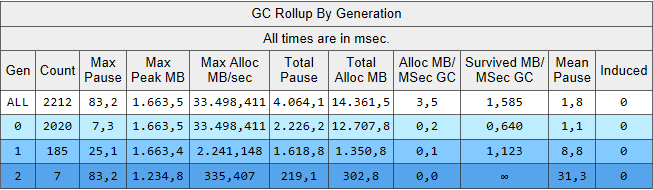
GCStats running CalculateWithImmutableQueueList, window size 15
GCStats beim Rufen von CalculateWithImmutableQueueList mit Fensterbreite 1500 und 10⁷ Zahlen.
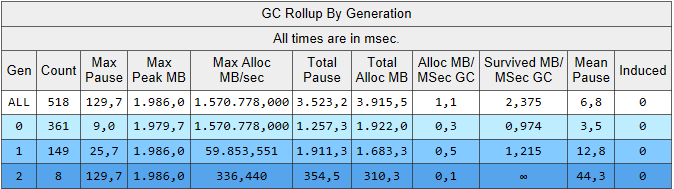
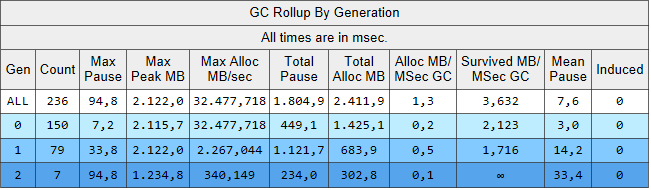
GCStats for CalculateWithImmutableQueueList, window size 150
GCStats beim Rufen von CalculateWithImmutableQueueStack mit Fensterbreite 1500 und 10⁷ Zahlen.
GCStats for CalculateWithImmutableQueueList, window size 150
GCStats beim Rufen von CalculateWithQueueStack mit Fensterbreite 1500 und 10⁷ Zahlen.

In der Rechnung, die CalculateWithImmutableQueueList ruft arbeitet die GC in Generation 0 etwa sechs mal so oft als in der Rechnung, die CalculateWithImmutableQueueList ruft. Aufsammeln mit dem veränderlichen Stapel spart noch mehr GC durch mehr wiederverwendeten Speicher.

In Fällen, in denen viele Werte aufgesammelt werden müssen, ist der unveränderliche Stapel schneller als die unveränderliche Liste. Ist die Rechendauer wichtig, sollte man den veränderlichen Stapel in Betracht ziehen. Im obigen Beispiel waren sowohl das Fenster und der Aufsammler lokal und nicht sichtbar in der öffentlichen Signatur. Bibliotheksnutzer nähmen also von der Wahl nur indirekt Notiz. Für jene die am privaten Quelltext arbeiten ist die Wahl nicht irrelevant. In Fällen, in denen die Rechendauer nicht so wichtig ist, ist die Wahl mehr eine Stilfrage und dann überwiegen die Vorzüge unveränderlicher Sammlungen.