Rico Erhard, Immutable collections, GC overhead.

This text is about immutable collections, presents an example calculation in which they are used and compared to mutable collections.

Immutable collections are useful for writing pure functions. Pure functions are thread safe and tend to be easy to test. One property of pure functions is that they do not mutate their arguments. That property is evident in function signatures that use immutable parameters only.

For example, the following function signature


using System;
using System.Collections.Immutable;
...
public static ImmutableList<double> CalculateSomething(ImmutableList<double> input, int windowSize)
...

emphasizes that the calculation, whatever it may calculate, does not mutate the given input.

Adding values to an immutable list can be done through calling its Add method. This creates a new list with the added value and does not change the original list. This scheme is common to other immutable types. And if the original collection stays unreferenced it will be garbage collected. Creating changed immutable collections many times creates many unused collections to be garbage collected. This can lead to a noticable performance impact as demonstrated by Hadi Brais in the MSDN magazine.

A case where this happens is to calculate the simple moving averages of a sequence of 10 million floating point numbers with a window size of 1500. To calculate the simple moving averages, it is necessary to keep track of the values moving window. A queue is a convenient collection to store the window. Lists and stacks are convenient for accumulating the averages. The public functions in the following code perform this calculation with different collection types.

using System;
using System.Linq;
using System.Collections.Generic;
using System.Collections.Immutable;

namespace MovingAverage
{
    public static class Calculator
    {
        public static ImmutableList<double> CalculateWithImmutableQueueList(int windowSize, ImmutableList<double> input)
        => CalculateWithImmutableQueue(
            ImmutableList.Create<double>(),
            (list, next) => list.Add(next),
            windowSize,
            input).ToImmutableList();

        public static ImmutableList<double> CalculateWithImmutableQueueStack(int windowSize, ImmutableList<double> input)
        => CalculateWithImmutableQueue(
            ImmutableStack.Create<double>(),
            (stack, next) => stack.Push(next),
            windowSize,
            input).Reverse().ToImmutableList();

        public static ImmutableList<double> CalculateWithImmutableQueueAndMutableStack(int windowSize, ImmutableList<double> input)
        => CalculateWithImmutableQueue(
            new Stack<double>(),
            (stack, next) => { stack.Push(next); return stack; },
            windowSize,
            input).Reverse().ToImmutableList();

        public static ImmutableList<double> CalculateWithImmutableQueueAndMutableList(int windowSize, ImmutableList<double> input)
        => CalculateWithImmutableQueue(
            new List<double>(),
            (list, next) => { list.Add(next); return list; },
            windowSize,
            input).ToImmutableList();

        public static ImmutableList<double> CalculateWithQueueStack(int windowSize, ImmutableList<double> input)
        => CalculateWithMutableQueue(
            new Stack<double>(),
            (stack, next) => { stack.Push(next); return stack; },
            windowSize,
            input).Reverse().ToImmutableList();

        public static ImmutableList<double> CalculateWithQueueList(int windowSize, ImmutableList<double> input)
        => CalculateWithMutableQueue(
            new List<double>(),
            (list, next) => { list.Add(next); return list; },
            windowSize,
            input).ToImmutableList();

        static S CalculateWithImmutableQueue<S>(S emptyStack, Push<S> push, int windowSize, ImmutableList<double> input)
        => Calculate(
            ImmutableQueue<double>.Empty,
            (queue) => queue.Peek(),
            (queue, next) => queue.Enqueue(next),
            (queue) => queue.Dequeue(),
            emptyStack,
            push,
            windowSize,
            input);

        static S CalculateWithMutableQueue<S>(S emptyStack, Push<S> push, int windowSize, ImmutableList<double> input)
        => Calculate(
            new Queue<double>(),
            (queue) => queue.Peek(),
            (queue, next) => { queue.Enqueue(next); return queue; },
            (queue) => { _ = queue.Dequeue(); return queue; },
            emptyStack,
            push,
            windowSize,
            input);

        static S Calculate<Q, S>(
            Q emptyQueue,
            Peek<Q> peek,
            Enqueue<Q> enqueue,
            Dequeue<Q> dequeue,
            S emptyStack,
            Push<S> push,
            int windowSize,
            ImmutableList<double> input)
        {
            IEnumerable<double> head = input.Take(windowSize - 1);
            ImmutableList<double> tail = input.TakeLast(input.Count - (windowSize - 1)).ToImmutableList();

            Q headQueue = head.Aggregate(emptyQueue, (q, next) => enqueue(q, next));

            return tail.Aggregate((head.Sum(), headQueue, emptyStack), (state, next) =>
            {
                double sum = state.Item1 + next;
                Q queue = state.Item2;
                S stack = state.Item3;

                stack = push(stack, sum / windowSize);

                sum -= peek(queue); 
                queue = dequeue(queue);
                queue = enqueue(queue, next);

                return (sum, queue, stack);
            }).Item3;
        }

        delegate S Push<S>(S stack, double next);

        delegate Q Enqueue<Q>(Q queue, double next);

        delegate Q Dequeue<Q>(Q queue);

        delegate double Peek<Q>(Q queue);
    }
}

The bulk of the calculation is performed by of the private Calculate function that takes several delegates to accomodate for the different interfaces of the collection types to

peek the oldest element of the window,
enqueue window elements,
dequeue window elements and to
push the averages to an accumulator.

Note that pushing the averages to a stack requires a reversal to yield the averages in the correct order.

The following code contains a test that checks the correctness of the calculation and a test that prints the duration of each calculation.

using System;
using System.Collections.Generic;
using System.Collections.Immutable;
using System.Linq;
using Xunit;
using static Xunit.Assert;
using static MovingAverage.Calculator;
using System.Diagnostics;
using static System.Diagnostics.Stopwatch;
using Xunit.Abstractions;
using System.Collections;

namespace MovingAverage.Test
{
    public class CalculatorTest
    {
        readonly ITestOutputHelper output;
        public CalculatorTest(ITestOutputHelper output)
        {
            this.output = output;
        }

        [Theory]
        [ClassData(typeof(TestArguments))]
        public void CheckMath(SmaCalculator smaCalculator, int windowSize)
        {
            const int n = 10_000;

            ImmutableList<double> input = GetRandomNumbers(n, -1, 1).ToImmutableList();
            ImmutableList<double> result = smaCalculator(windowSize, input);

            Equal(input.Count() - windowSize + 1, result.Count());
            Equal(input.Take(windowSize).Sum() / (double)windowSize, result.First(), 6);
            Equal(input.TakeLast(windowSize).Average(), result.Last(), 6);
        }

        [Theory]
        [ClassData(typeof(TestArguments))]
        public void MeasureDuration(SmaCalculator smaCalculator, int windowSize)
        {
            const int n = 10_000_000;

            ImmutableList<double> input = GetRandomNumbers(n, -1, 1).ToImmutableList();
            Measure(n, windowSize, () => _ = smaCalculator(windowSize, input));

            void Measure(int n, int k, Action calc)
            {
                Stopwatch sw = StartNew();
                calc();
                sw.Stop();
                double elapsedSeconds = sw.ElapsedMilliseconds / 1000.0;
                output.WriteLine("Calculating the moving averages with "
                    + $"{smaCalculator.Method.Name}, n = {n.ToString("e0")}, k = {k} took {elapsedSeconds.ToString("N3")}s.");
            }
        }

        public class TestArguments : IEnumerable<object[]>
        {
            public IEnumerator<object[]> GetEnumerator()
            {
                foreach (var p in GetParametersWithWindowSize(15)) yield return p;
                foreach (var p in GetParametersWithWindowSize(150)) yield return p;
                foreach (var p in GetParametersWithWindowSize(1500)) yield return p;
            }

            IEnumerable<object[]> GetParametersWithWindowSize(int windowSize)
            => ImmutableList.Create<object[]>
            (
                new object[] { (SmaCalculator)CalculateWithImmutableQueueList, windowSize },
                new object[] { (SmaCalculator)CalculateWithImmutableQueueStack, windowSize },
                new object[] { (SmaCalculator)CalculateWithImmutableQueueAndMutableStack, windowSize },
                new object[] { (SmaCalculator)CalculateWithImmutableQueueAndMutableList, windowSize },
                new object[] { (SmaCalculator)CalculateWithQueueStack, windowSize },
                new object[] { (SmaCalculator)CalculateWithQueueList, windowSize }
            );

            IEnumerator IEnumerable.GetEnumerator() => GetEnumerator();
        }

        static IEnumerable<double> GetRandomNumbers(int count, double from, double to)
        {
            Random r = new Random(0);
            return Enumerable.Range(0, count).Select(_ => from + (to - from) * r.NextDouble());
        }

        public delegate ImmutableList<double> SmaCalculator(int windowSize, ImmutableList<double> input);
    }
}

The duration of a run were

CalculateWith	window size 15	window size 150	window size 1500
ImmutableQueueList	11.4s	13.1s	11.6s
ImmutableQueueStack	5.4s	5.6s	5.4s
ImmutableQueueAndMutableStack	4.2s	3.8s	3.7s
ImmutableQueueAndMutableList	3.7s	3.8s	3.6s
QueueList	3.2s	3.4s	3.3s
QueueStack	3.2s	3.6s	3.3s

Accumulating with an immutable list takes longer than accumulating with an immutable stack The reason is already explained by Hadi Brais in the previously mentioned article. The immutable stacks are implemented as a GC-friendly linked list while the immutable list is implemented as a binary tree. Appending nodes to that tree

requires traversing the tree,
performs tree rotations,
triggers the GC.

To see the increased GC activity, I collected the GCStats of three calculations with PerfView.

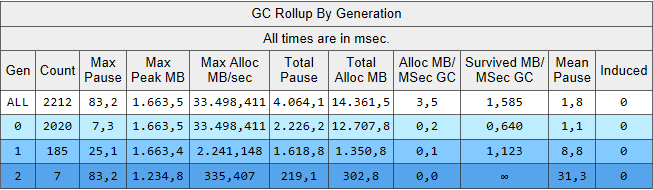
GCStats running CalculateWithImmutableQueueList, window size 15 — GCStats calling CalculateWithImmutableQueueList with window size 1500 and 10⁷ numbers.

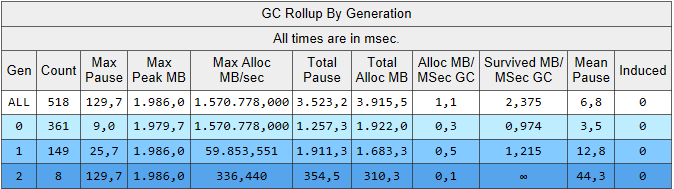
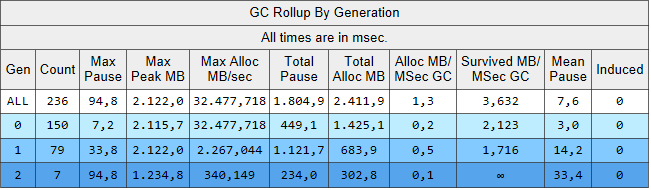
GCStats for CalculateWithImmutableQueueList, window size 150 — GCStats calling CalculateWithImmutableQueueStack with window size 1500 and 10⁷ numbers.

In the calculation that calls CalculateWithImmutableQueueList the heap generation 0 is garbage collected about six times more often as compared to the calculation that calls CalculateWithImmutableQueueList. When accumulating with the mutable stack in the calculation that calls CalculateWitheQueueStack memory reuse is higher, garbage collection lower.

In the calculation that calls CalculateWithImmutableQueueList So, if performance is a concern, accumulating many items with an immutable stack is better than the immutable list. If performance is of high importance, mutable collections are better. In the given example calculation, the accumulator and the window collection are local. They do not appear in the public signature. Choosing one over the other does not matter for a library consumer. But the choice matters for programmers who maintain the private sections of code. In cases where performance is not critical, the choice is more a question of style and the benefits of immutable collections outweigh their performance overhead.